Locally-Weighted CNMP
CNMP, and how to solve it’s weaknesses:
CNMP is a learning-from-demonstration model that can given the conditions,(task specific information, positions at certain time) create a trajectory where each point in time is represented with a mean and and standard deviation(how unsure the model is):
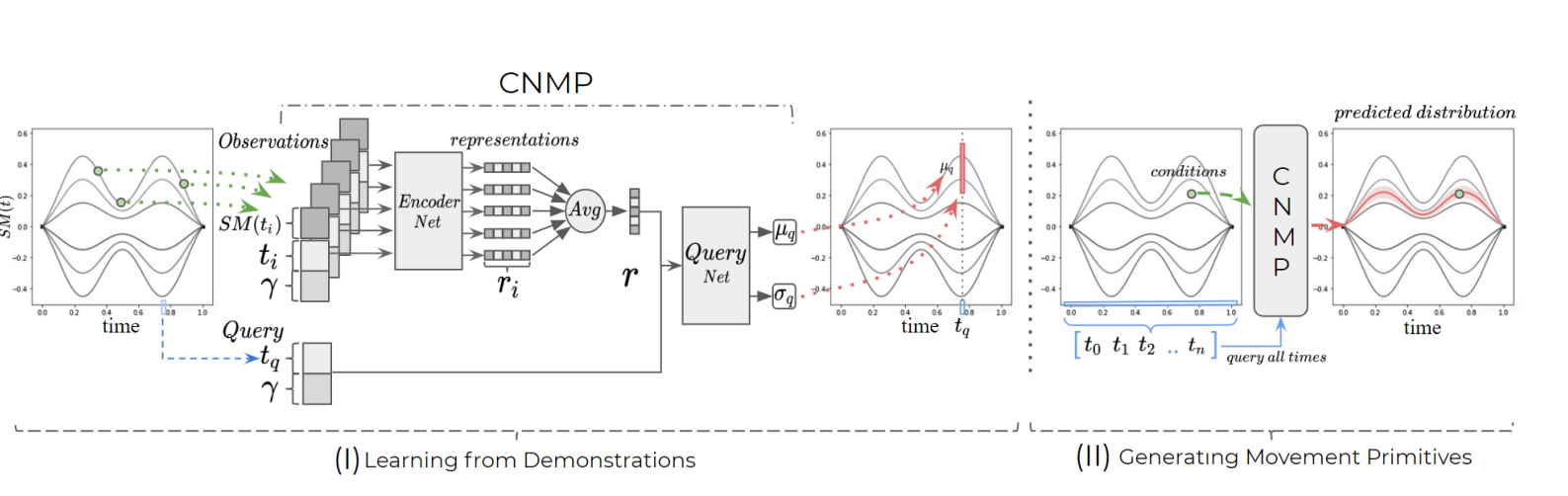
For each condition point the encoder creates a latent vector, and after every condition point is encoded in latent space, these vectors are aggregated. Aggregated vector is concatenated with the query time point and the decoded vector output becomes the trajectory output at that certain time.
I initally wanted to implement attentive version of the CNMP by changing the encoder. The architecture I implemented was like this:
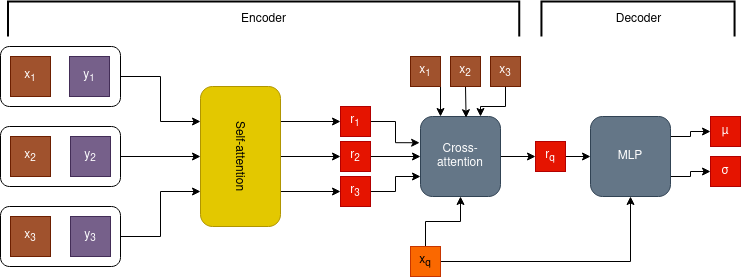
We have compared the model with CNMP in a box pushing environment. The reward points were calculated by accumulation of how close the box is to the target point through time.
The reward plots showed a dominant performance boost over the vanilla-CNMP.
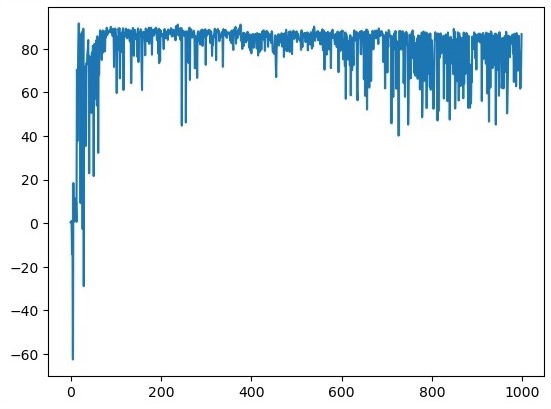
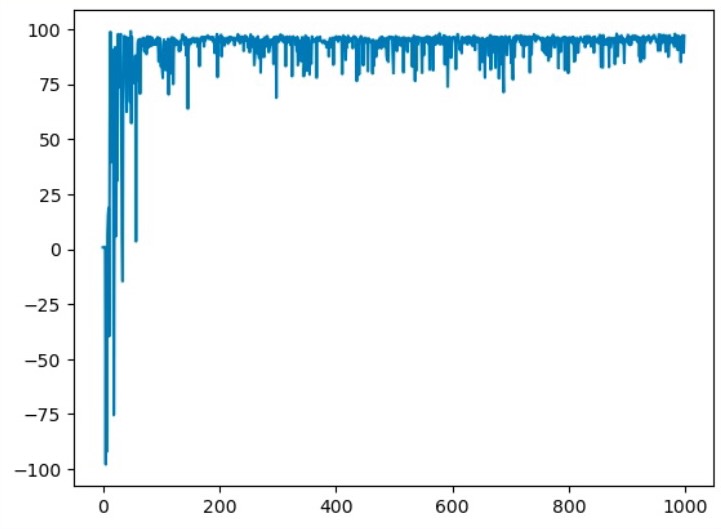Reward through time: CNMP(left) vs Attention-CNMP
I knew that we can further improve CNMP in areas such as:
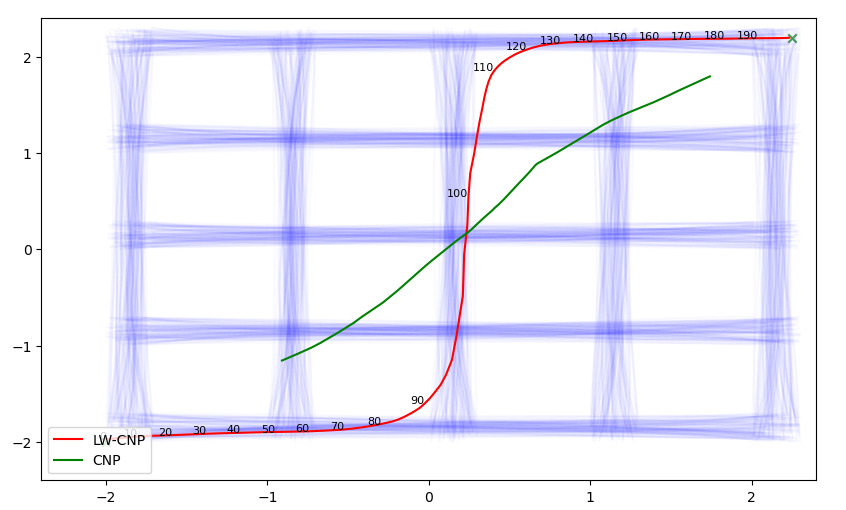
- Blending: Since you want to find the trajectory that is represented by condition points, if the trajectory is a mixture of primitives,the model fails. You can see it in the figure below. When you teach the orange and blue demonstrations to the model, the trajectory is guessed wrong if you give the start of the orange and the end as blue.
The solution we thought is that, we can aggregate the latent vectors in a way that queried points should be affected by closer conditions more.
The equation given is:
\[r(t) = \frac{\sum w_n \cdot r_{c_n}}{\sum w_n} \quad \text{where} \quad w_n = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(r_{c_n} - \mu_t)^2}{2\sigma^2}}\] \[\begin{align*} &\text{where:} \\ &\text{- } r(t) \text{ represents the weighted sum at time } t. \\ &\text{- } w_n \text{ is the weight for each component } r_{c_n}. \\ &\text{- } \mu_t \text{ and } \sigma \text{ represent the mean and standard deviation of the Gaussian distribution, respectively.} \\ &\text{- The exponential term } e^{-\frac{(r_{c_n} - \mu_t)^2}{2\sigma^2}} \text{ is the Gaussian probability density function,} \\ &\text{ which calculates the weight } w_n \text{ for each component based on its distance from the mean } \mu_t. \\ &\text{- The sum } \sum w_n \cdot r_{c_n} \text{ calculates the weighted sum of the components, and this sum} \\ &\text{ is then normalized by dividing by the sum of the weights } \sum w_n. \end{align*}\]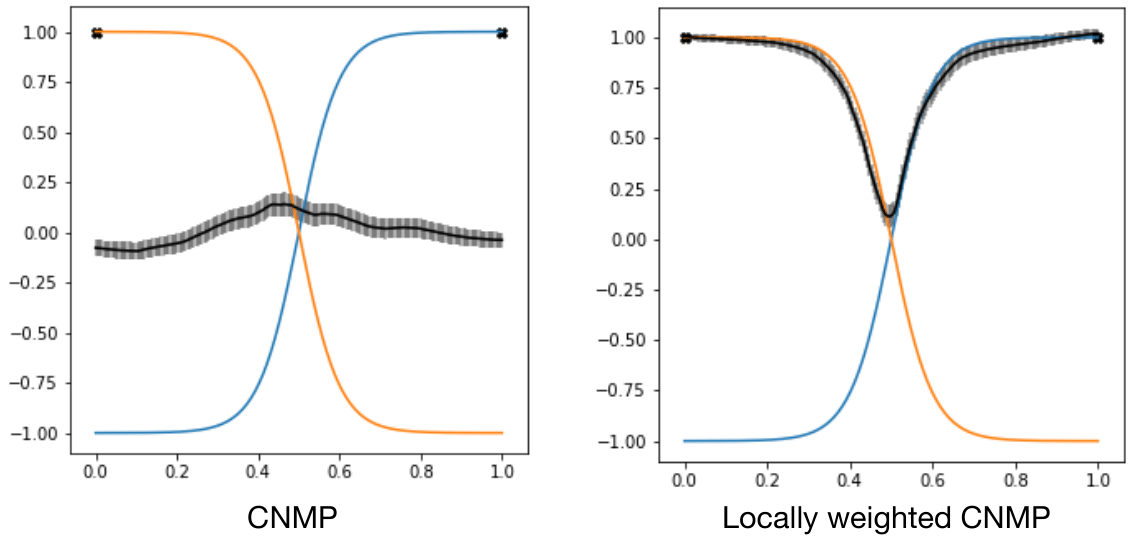
- Multimodality: Basicly when you represent each point as a gaussian distribution, you cannot represent multimodal distributions. Think it this way, If your demonstrations are only going vertical and going horizontal from a certain position,the model will learn to go diagonally given there are same amount of diagonal and horizontal demonstrations. My solution for this part was to implement a vector quantized model.
- Initialize memory vectors in arbitrary number bigger than the amount of different primitives you will show.
- The model will be trained in a way to compare the encoded latent vector to memory vectors and get similarity score by taking dot product of the vectors.
- Select the closest demonstration from the memory and execute it.
- Uncertainity: Information doesn’t necessarily have to be complete. In CNMP, your conditioning points needs to give every type of information while training. So basically, I will train the model to have a drop out at the initial layer depending on a condition. This way I can also execute a correctifying trajectory between the condition points, to avoid high deviation jumps while transitioning between trajectories. This part is why I still didn’t published a paper.
Meanwhile, we can use the current model to creates a dance choreography by teaching every dance move seperately like the image below: